Section 1.1: Focusing on Solar Radiation Pressure

With a fundamental understanding established, let’s specifically focus on the perturbation caused by solar radiation pressure (SRP). By the conclusion of this article, we aim to derive an expression that models the motion of a minor mass influenced by both solar radiation pressure and the gravitational force from a significant body, such as a planet, moon, or star. For those unfamiliar with the two-body problem (2BP), I recommend reviewing the linked article that elaborates on the derivation of the equations we will utilize as the foundation for our new model.

This video provides insights into the theory of solar radiation pressure (SRP) and its implications in orbital mechanics, particularly using Python.

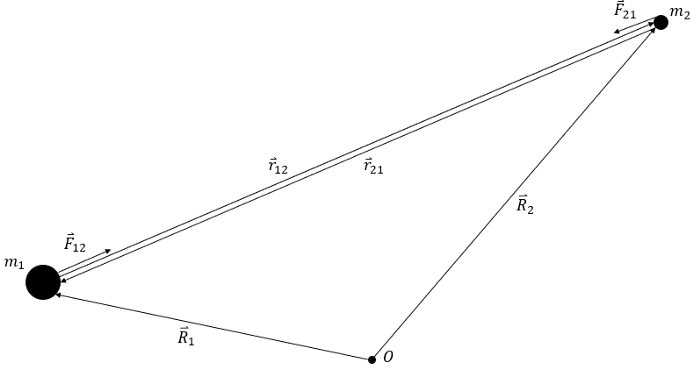
For the remainder of this discussion, I will refer to our primary significant body as Earth and the mass of interest as a satellite. However, these concepts can be universally applied to any significant mass and a smaller, negligible mass. Below is a diagram illustrating the two-body problem alongside the equations of motion relevant to this system:

The equations of motion are given by:

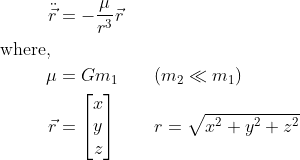
Here, the vector r, composed of x, y, and z coordinates, indicates the position of the satellite relative to the Earth (the primary mass). The universal gravitational constant is denoted by G, m? represents Earth’s mass, and m? signifies the satellite’s mass. The gravitational parameter is symbolized by ?. For the sake of simplicity, we generally disregard the mass of the satellite, as it is minuscule compared to that of Earth. As stated earlier, we will use the two-body problem as a foundation from which we will incorporate solar radiation pressure perturbations.

Section 1.2: Understanding Solar Radiation Pressure

Solar radiation pressure is the mechanical force exerted by electromagnetic waves. Although these waves are devoid of mass, they possess mass-like characteristics, such as momentum. Consequently, the photons emitted by the Sun carry momentum and can transfer that momentum to massive objects. While this momentum is relatively minute, it still influences orbital dynamics. The impact of solar photons is most pronounced on objects that have a large surface area, are highly reflective, are in close proximity to the Sun, and have a low mass.

The following equation describes the radiation pressure resulting from the Sun:

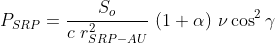
In this formula, S? represents the Sun’s irradiance at 1 AU (astronomical unit), or the solar constant, which is approximately 1361 W/m² at the average distance between the Earth and the Sun. The speed of light is denoted by c (299,792,458 m/s), and r?????? signifies the distance from the Sun to the satellite (in AU). The parameter ? indicates the reflectivity coefficient of the satellite, ranging from 0 (non-reflective) to 1 (perfectly reflective). The ? symbol reflects an eclipse factor, determining whether the satellite is in the shadow of the primary mass. Lastly, ? signifies the angle of incidence of the Sun’s rays relative to the satellite’s surface.

To quantify the effect of solar radiation pressure on the satellite’s acceleration, we multiply the equation above by the surface area and divide by the satellite’s mass. This calculation yields the force generated by the pressure and subsequently the acceleration magnitude.

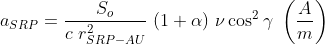
In this context, A and m symbolize the effective cross-sectional area and mass of the satellite. To assess how this acceleration impacts the two-body problem, we need to adjust our original diagram and equations to reflect this additional force. The next diagram includes the Sun to illustrate the distances between the Earth, Sun, and satellite (excluding the gravitational effect of the Sun).

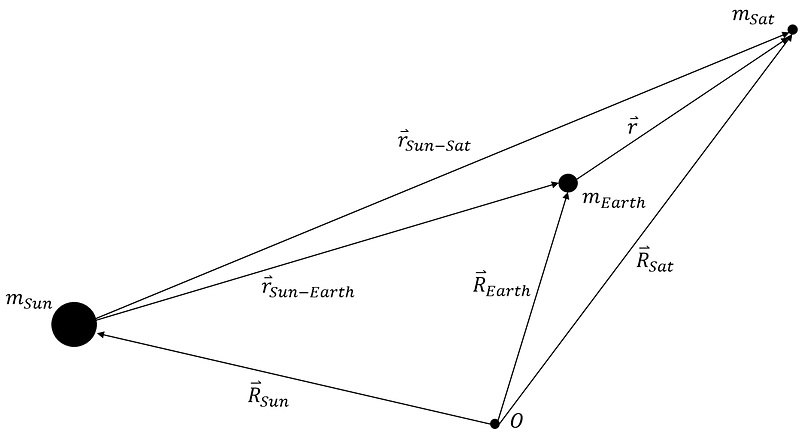
This diagram contains multiple vectors; I will provide a brief overview of its components. The uppercase R vectors depict the positions of the Sun, Earth, and satellite relative to an inertial reference point. This inertial frame is crucial for applying Newton’s second law, which forms the basis for deriving the equations of motion for the two-body problem. The lowercase r vectors illustrate the positions of one mass concerning another. Our primary focus is on the lowercase r vector without any label, which represents the satellite's motion relative to the Earth.

To incorporate perturbing forces into the two-body problem, one can simply add their effects to the original equations of motion, as shown below:

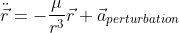
Now, we will express our acceleration in vector form and apply it to the previous equation. The acceleration vector will align with the position vector extending from the Sun to the satellite. By combining the acceleration magnitude equation with a unit vector along this position vector, we can define the acceleration vector:

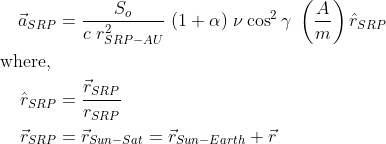
By merging the two equations discussed above, we derive the following result, which describes the equations of motion for a satellite influenced by a single massive body and solar radiation pressure.

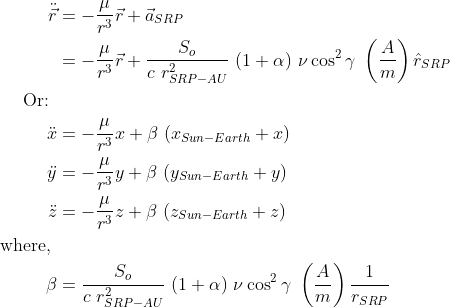
It's important to note that knowing the position of the Earth relative to the Sun is crucial for utilizing these equations, which can complicate simulations. The following illustration depicts the variation in a satellite's orbit around the Earth due to solar radiation pressure.

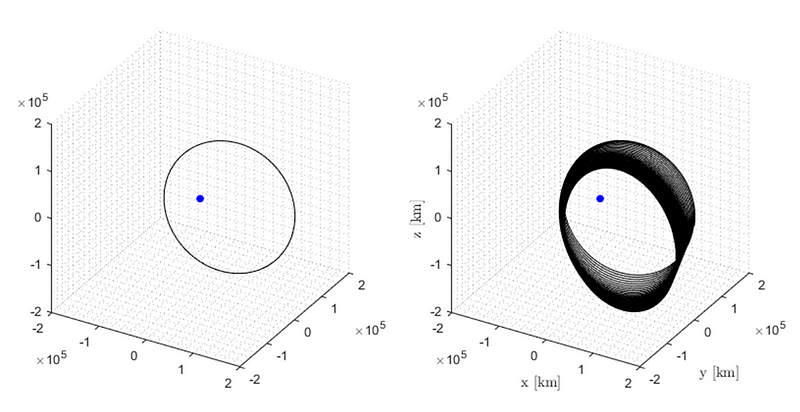
The image contrasts a simple two-body orbit (left) with a two-body orbit that includes solar radiation perturbations (right). As illustrated, solar radiation pressure can significantly alter a satellite's trajectory in this simulation. While this example may be exaggerated, the effects are relevant for all satellites. I plan to write another article soon that will detail how to simulate these equations and share tips that could simplify the process, including how to determine the Earth’s position relative to the Sun. Once completed, I will provide a link here.

This approach represents one of the more straightforward methods for calculating the impact of radiation pressure. Numerous complex studies on this subject exist, which I encourage you to explore further. The equations and methodologies outlined here will offer a solid estimate of how an orbit might evolve over time when considering solar radiation pressure. Thank you for reading! I hope you found this information enlightening. Please give a clap and follow if you're interested in learning more about orbital mechanics, coding, and machine learning!