Testing for Primality

One common primality test is as follows:

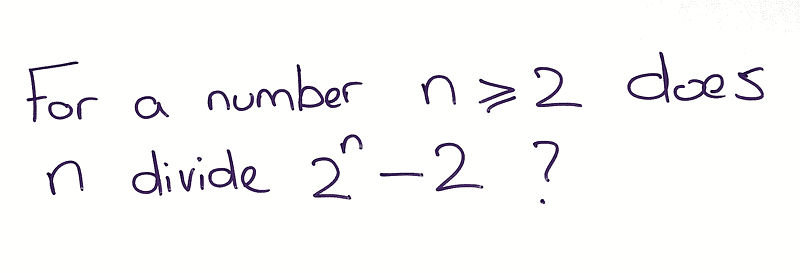
If the result is 'no', it confirms that n is not a prime number. This is derived from Fermat’s Little Theorem, which asserts that if p is a prime, then:

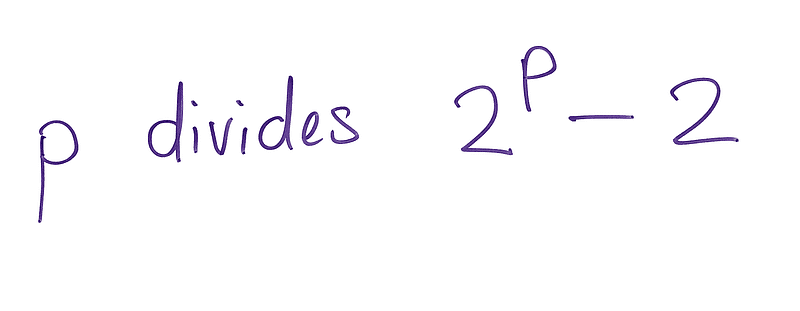
To demonstrate this, we can apply it to the first few primes:

• For p=2: 2 divides (2^2-2=4-2=2 times 1)
• For p=3: 3 divides (2^3-2=8-2=6=3 times 2)
• For p=5: 5 divides (2^5-2=32-2=30=5 times 6)
• For p=7: 7 divides (2^7-2=128-2=126=7 times 18)
• For p=11: 11 divides (2^{11}-2=2048-2=2046=11 times 186)
• For p=13: 13 divides (2^{13}-2=8192-2=8190=13 times 630)

If the answer is 'yes', we cannot definitively conclude if n is prime or composite. However, we will explore below that a 'yes' response often indicates a high probability that n is prime!

Base 2 Pseudoprimes

In 1819, French mathematician Pierre Frédéric Sarrus noted that the smallest composite number n for which the above test yields 'yes' is 341.

He demonstrated that 341 (which equals 11 multiplied by 31) divides (2^{341}-2).

You may wonder how mathematicians manage calculations involving large numbers like (2^{341}); modular arithmetic facilitates this process, which you can learn more about here.

For entertainment, I wrote a simple Python script (see below) to identify numbers less than (10^5) that yield 'yes' for the above test.

It shows that among the numbers checked, 9592 are prime, while 78 are composite, indicating that an overwhelming 99.19% were indeed prime.

Here are the 78 composite numbers found:

341, 561, 645, 1105, 1387, 1729, 1905, 2047, 2465, 2701, 2821, 3277, 4033, 4369, 4371, 4681, 5461, 6601, 7957, 8321, 8481, 8911, 10261, 10585, 11305, 12801, 13741, 13747, 13981, 14491, 15709, 15841, 16705, 18705, 18721, 19951, 23001, 23377, 25761, 29341, 30121, 30889, 31417, 31609, 31621, 33153, 34945, 35333, 39865, 41041, 41665, 42799, 46657, 49141, 49981, 52633, 55245, 57421, 60701, 60787, 62745, 63973, 65077, 65281, 68101, 72885, 74665, 75361, 80581, 83333, 83665, 85489, 87249, 88357, 88561, 90751, 91001, 93961.

Thus, we can interpret this as a probabilistic method for determining primality; if an odd number n answers 'yes', we can assert with high confidence that it is prime, although it is not a guarantee.

Note that even numbers can be disregarded, as the only even prime is 2.

Consequently, the composite numbers identified above are termed (Base 2) Pseudoprimes, which are relatively rare compared to actual primes.

In mathematical terms, n is a (Base 2) Pseudoprime if it is composite and satisfies the congruence relation (2^n equiv 2 mod n) (where '^' denotes exponentiation).

Here, the notation (a equiv b mod m) signifies that m divides the difference between a and b.

These numbers are also known as (Base 2) Fermat Pseudoprimes, Sarrus Numbers, or Poulet Numbers.

In 1938, Belgian mathematician Paul Poulet compiled a list of such numbers below (10^5), an impressive feat for his time without the aid of modern computing technology.

Are There Infinitely Many (Base 2) Pseudoprimes?

Yes, Malo demonstrated in 1903 that if n is a (Base 2) Pseudoprime, then so is (2^n-1).

For example, since 341 is a (Base 2) Pseudoprime, it follows that (2^{341}-1) is also a (Base 2) Pseudoprime.

By continuing this process, it becomes evident that there are infinitely many such numbers.

Are There Even (Base 2) Pseudoprimes?

While it’s clear that any even number greater than 2 cannot be prime, it raises the question of whether an even pseudoprime exists.

Indeed, the smallest example is 161038, calculated as (2 times 73 times 1103), which divides (2^{161038}-2).

This was established by American mathematician Derrick Lehmer in 1950.

Furthermore, in 1951, Dutch mathematician Nicolaas Beeger proved that infinitely many even (Base 2) Pseudoprimes exist.

How Close Are (Base 2) Pseudoprimes to Being Prime?

One can consider a composite number as being closer to a prime if it is formed from fewer prime factors.

For example, 341 (11 x 31) is closer to being prime than 541 (3 x 11 x 17), which has three prime factors.

In 1949, Erdos demonstrated that for every integer (k geq 2), there exist infinitely many pseudoprimes made from exactly k distinct primes.

Python Script to Identify (Base 2) Pseudoprimes

from math import sqrt

def mod_calculator(base, power, modulo):

return base ** power % modulo

def fermats_little_theorem_test(base, number):

return mod_calculator(base, number, number) == base

def is_prime(number):

if number <= 1:

return False

if number == 2:

return True

if number % 2 == 0:

return False

for integer in range(2, int(sqrt(number) + 1)):

if number % integer == 0:

return False

return True

base = 2

max_limit = 100000

pseudoprime_count = 0

actualprime_count = 0

pseudoprime_list = []

for integer in range(2, max_limit):

if is_prime(integer):

actualprime_count += 1

elif fermats_little_theorem_test(base, integer):

pseudoprime_list.append(integer)

pseudoprime_count += 1

print("Number of actual primes: ")

print(actualprime_count)

print("Number of Base 2 Pseudoprimes: ")

print(pseudoprime_count)

print("Percentage of primes: ")

print(actualprime_count / (actualprime_count + pseudoprime_count))

print(pseudoprime_list)

Note: The Sieve of Eratosthenes was utilized to verify prime status; you can read more about it here.

Closing Remarks on Carmichael Numbers

In the subsequent section, we will delve into more generalized pseudoprime numbers known as Carmichael Numbers.

These are even less common than (Base 2) Pseudoprimes and enable the development of more robust tests to enhance our confidence in identifying prime numbers.

References

[1] Chapter 8 Pseudoprimes in "The Little Book Of Big Primes" by Paulo Ribenboim

This video discusses Fermat's theorem, pseudoprimes, and their representation in popular culture, such as in the show Futurama.

This video provides a comprehensive overview of Fermat pseudoprime numbers and their significance in number theory.