The Mathematical Legacy of Georg Cantor: Unraveling Infinity
Written on
Chapter 1: Understanding Infinite Cardinalities
In my previous article, I left you with an intriguing puzzle regarding the intricate nature of infinity. Today, we will delve deeper into the concepts of Aleph and Beth numbers, elucidating their distinctions and exploring the infinite hierarchies they represent.
Both Aleph and Beth numbers describe infinite cardinalities, but they serve different purposes. As discussed earlier, when we consider the set of all possible subsets of a given set, we generate a new set known as the Powerset. Remarkably, this Powerset is always larger than the original set, regardless of whether the original is finite or infinite.
A cardinal number can be defined as a class of sets that can be matched one-to-one with one another. Since the Powerset of any set belongs to a cardinal class that is strictly larger than that of the original set, we can construct an infinite hierarchy of cardinal numbers systematically:

Beth zero corresponds to Aleph zero, representing the smallest infinite cardinality, which can be put in one-to-one correspondence with the natural numbers. By applying the Powerset operation repeatedly, we can establish a hierarchy of increasingly large Beth numbers. The notation for the Powerset of a set X is denoted as 2^X, which is intuitive since each element of the original set has two possibilities: it can either be included or excluded from the set. Therefore, the size of the Powerset is always represented as 2^X, even for infinite sets.
Conversely, Georg Cantor initiated his exploration with Aleph zero and provided a non-constructive proof asserting that every cardinal has a uniquely larger successor. This concept gives rise to a sequence of cardinals, akin to how integers are enumerated via the Peano axioms, with one notable exception: a "break" occurs at Aleph zero. Consequently, Cantor's findings allow us to list his cardinals in a discrete sequence:
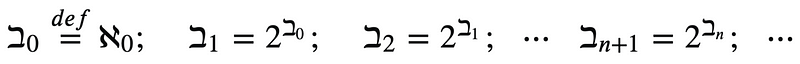
While there are additional "breaks" and larger limit cardinals, the ones we've examined raise a compelling question: Are there infinite Aleph cardinals that do not correspond to Beth cardinals? This inquiry leads us to the famous Continuum Hypothesis.
Section 1.1: The Continuum Hypothesis Explained
The original form of the Continuum Hypothesis posed a straightforward question: are there any infinite cardinals between Aleph zero (the size of the integers) and the cardinality of the reals? This question is fundamentally equivalent to our earlier query.
The esteemed mathematician Kurt Gödel advanced this discussion by demonstrating that the existence of cardinals between Aleph zero and Aleph one cannot be disproven using the axioms of Zermelo-Fraenkel set theory (ZFC). Gödel's 1938 results, a continuation of his First Incompleteness Theorem, established a pivotal principle in logic, which was further expanded upon by Paul Cohen in 1963. Cohen proved that the existence of these cardinals cannot be proven either, rendering the question independent of ZFC.
In essence, we can either assume or reject the existence of non-Beth Aleph cardinals as an axiom, and both stances are logically consistent with ZFC and the Peano postulates. This situation introduces concepts of unprovability and decidability into mathematics, distinct from mere truth or falsehood.
Subsection 1.1.1: The Independence of the Axiom of Choice
Cohen's work also established that the Axiom of Choice is independent of Zermelo-Fraenkel set theory, creating a mathematical model that satisfies ZF and C. Thus, the Axiom of Choice cannot be derived from Zermelo-Fraenkel set theory alone.
Now, let us explore some fascinating examples of undecidability that stem from Cantor's groundbreaking ideas.
The video title is "Georg Cantor is the father of all mainstream mathematical cranks and clowns." This video discusses the complexities and controversies surrounding Cantor's work and its impact on the field of mathematics.
Chapter 2: The Undecidable and Uncomputable Realm
Cantor's ideas have inspired profound investigations into the foundations of mathematics, leading to a realm filled with the strange and unexpected. This exploration reveals the intricacies of undecidable and uncomputable problems, challenging our understanding of mathematical truth.
References
- John Stillwell, “The Real Numbers: An Introduction to Set Theory and Analysis”, Springer, 2013
- John Stillwell, “Roads to Infinity: The Mathematics of Truth and Proof”, A K Peters/CRC Press 2011
- George E. Witter, “Mathematics: The Study of Axiom Systems”, Blaisdell Publishing Company, 1964
- Jean van Heijenoort, “From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931” (1967), Harvard University Press; Fourth Printing Edition (2002)