The Importance of Kretschmann Scalar in General Relativity
Written on
Understanding Singularities in General Relativity
Singularities present a profound mystery in the realm of physics, as they challenge our understanding of the universe. Roger Penrose aptly noted, “The greatest puzzle is the singularities because we don’t know what to do with them.” Black holes, for instance, obscure these singularities, where matter collapses to the extent that densities soar beyond comprehension. The physics governing such regions remains elusive, as the extreme conditions defy current theories.
The Kretschmann Scalar: A Fundamental Concept
The Kretschmann scalar, introduced by German physicist Erich Justus Kretschmann in his 1915 work “Über die prinzipielle Bestimmbarkeit der berechtigten Bezugssysteme beliebiger Relativitätstheorien,” serves as a vital tool in general relativity (GR). Kretschmann, born in Berlin and a student of Max Planck, contributed significantly to our understanding of spacetime curvature.
In the context of GR, the Kretschmann scalar (denoted as K) is essential for characterizing the curvature of spacetime. It is formulated from the Riemann curvature tensor, which describes how mass and energy warp spacetime.
The scalar is expressed mathematically as:
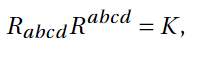
This quantity measures the curvature of spacetime at specific points and is invariant across different coordinate systems. While deriving the Kretschmann scalar may seem straightforward, practical applications often involve complex algebraic manipulations that can benefit from modern computational tools.
The Role of Kretschmann Scalar in Identifying Singularities
The Kretschmann scalar is crucial for distinguishing between different types of singularities in GR. Singularities indicate areas where curvature becomes infinite or where existing physical laws cease to apply. Visualize gravity compressing matter into an infinitesimally small point—such scenarios are theoretical, often occurring at the centers of black holes or during the Big Bang.
In GR, singularities are typically categorized into two types:
Curvature Singularities
These points in spacetime correspond to infinitely strong curvature. A prime example is the singularity at the heart of a Schwarzschild black hole, which cannot be removed and is fundamental to GR. Rotating black holes exhibit a different type of curvature singularity known as a Ring Singularity, which takes a circular form due to the black hole's angular momentum.
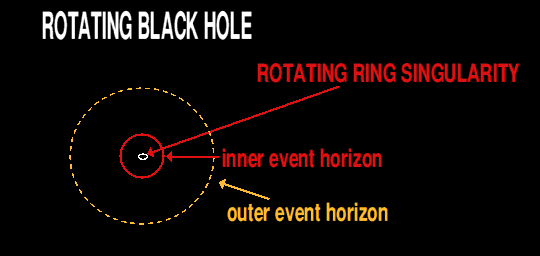
Coordinate Singularities
Unlike curvature singularities, these arise from specific coordinate choices and can be transformed or removed through different coordinate systems. An instance of this is the event horizon of a Schwarzschild black hole, where changing the coordinates can eliminate the perceived singularity.
Understanding the Kretschmann Scalar's Significance
The Kretschmann scalar’s ability to pinpoint the nature of singularities is vital. In the case of Schwarzschild spacetime, singularities are present at specific radii, illustrating the divergence of curvature at r = 0, which signifies a gravitational singularity.
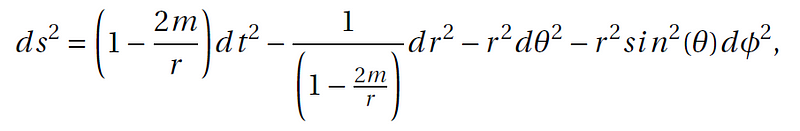
At r = 2m, however, the Kretschmann scalar remains finite, suggesting that this singularity may merely be a coordinate artifact rather than a true physical phenomenon.
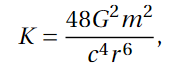
For the expanding universe described by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric, the Kretschmann scalar can be expressed through a specific equation, demonstrating its utility in understanding the universe's evolution.
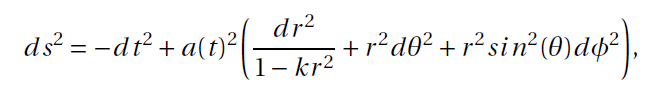
Conclusion: The Kretschmann Scalar's Universal Relevance
Ultimately, the Kretschmann scalar serves as a powerful indicator for identifying singularities across various spacetime contexts. Its independence from coordinate choices makes it a valuable tool for physicists seeking to understand the universe's most profound mysteries.
As we continue to explore these concepts, we hope to uncover more about black holes and the nature of singularities. Thank you for engaging with this discussion; feel free to share your thoughts or insights in the comments. Until next time, may you find success and happiness in your endeavors.
In the video titled "Kretschmann scalar - YouTube," viewers can delve deeper into the significance of this scalar in GR, providing further insight into its applications and implications.
The second video, "What is General Relativity? Lesson 59: Scalar Curvature Part 8 - YouTube," offers an educational overview of scalar curvature, enhancing the understanding of its role in general relativity.