At the core of modern AI research lies the challenge of enabling algorithms to generalize to new, unseen data. This capability is fundamental to machine learning, where models are typically trained and assessed under the assumption of i.i.d. (independent and identically distributed) data. This means that both training and testing datasets are derived from the same distribution, and generalization is achieved by discerning this common distribution solely from the training data.

However, this i.i.d. assumption often breaks down in real-world scenarios, where environments are dynamic, making out-of-distribution (o.o.d.) learning critical for adaptability and survival. Humans excel in this regard, swiftly identifying shifts in distributions and demonstrating few-shot learning, allowing us to deduce rules from minimal examples. In contrast, many classical ML models struggle with this flexibility; they often experience catastrophic forgetting, a phenomenon where neural networks entirely lose previously acquired knowledge when exposed to new data.

Generalization is intricately linked to the challenge of overfitting versus underfitting during training. Overfitting occurs when a model learns too much from the noise within the data rather than the actual signal. Techniques to mitigate overfitting include using models with fewer parameters, pruning, and applying regularization methods like dropout or L2 norms. Nevertheless, concepts around overfitting have been challenged by double descent, a phenomenon where high-capacity models initially perform worse than lower-capacity ones due to overfitting, but eventually outperform them as model capacity increases.

The generalization capabilities of large-scale transformer models, beginning with GPT-3's impressive performance on tasks outside its training, have further complicated our understanding of these concepts.

DeepMind's Flamingo advances this concept by merging language processing with vision models, enabling a wide array of vision-and-language tasks.

The capacity to represent knowledge in a generalized manner across tasks appears to be a hallmark of true intelligence, surpassing a neural network’s ability to classify animals after exposure to millions of labeled examples. The unexpected success of these advanced models raises intriguing questions regarding the essence of generalization and the mechanisms behind it: what precisely do these models learn? As their parameter counts approach those of human neurons, understanding their operation becomes increasingly complex. Are they merely adept at recalling all training data, or is there a deeper understanding at play?

Generalization is closely intertwined with memory; if we can extract meaning from data, we gain access to a more versatile and condensed representation of knowledge than simple recall allows. This is particularly vital in many unsupervised learning contexts, such as disentangled representation learning. The capacity for generalization is not only central to machine learning but also fundamental to various definitions of intelligence.

Markus Hutter posits that intelligence shares many traits with lossless compression, which is fittingly recognized through the Hutter Prize, awarded for advancements in compressing a specific text file of English Wikipedia. Together with Shane Legg, Hutter distilled a definition of intelligence from diverse sources in psychology, machine learning, and philosophy into a concise formula.

In simpler terms, intelligence can be viewed as an agent's ability to derive value from a multitude of environments, factoring in the complexity of those environments. The Kolmogorov complexity function serves as a measure of this complexity, indicating how intricate an object is by the shortest code needed to generate it. This ties back to the notion of intelligence as a form of efficient compression, where retaining noise necessitates memory, as noise lacks correlation and meaningful context.

Despite widespread acknowledgment of the importance of generalization in machine learning and its connection to complexity, quantifying it remains a challenge. A recent Google paper compiles over 40 measures aimed at characterizing complexity and generalization, yielding highly variable results.

The extent to which neural networks can generalize relates to their memory retention and their ability to learn to forget. Pedro Domingos’ recent paper titled “Every Model Learned by Gradient Descent Is Approximately a Kernel Machine” presents a fresh perspective on this issue:

> “Deep networks…are in fact mathematically approximately equivalent to kernel machines, a learning method that simply memorizes the data and uses it directly for prediction via a similarity function (the kernel). This greatly enhances the interpretability of deep network weights, by elucidating that they are effectively a superposition of the training examples.” — Pedro Domingos

Domingos highlights the mathematical similarities between learning in neural networks and kernel-based methods, such as Support Vector Machines.

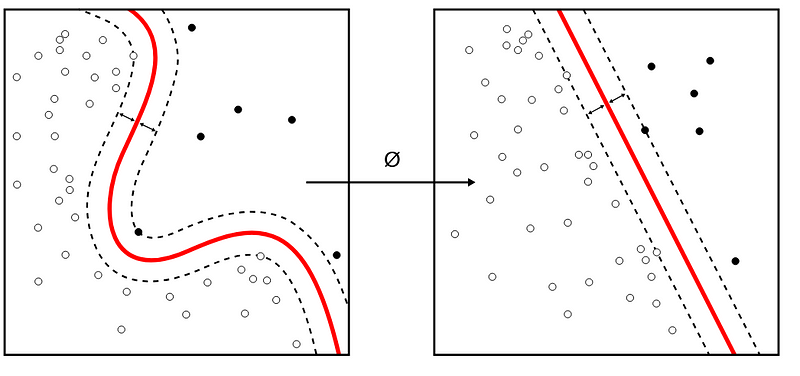
In essence, kernel-based methods first project the training data into a new space, termed the feature vector space, through a nonlinear transformation. Features in this space can possess intuitive characteristics (like the emotional tone of a movie), allowing for linear separability or k-nearest neighbor classification, where a test data point is compared with its nearest neighbors in the feature space to determine its classification.

Deep metric learning explores similar inquiries, seeking to establish embedding spaces where the similarity between samples is easily measurable, such as distinguishing unseen images of faces in face recognition tasks. Conversely, the neural tangent kernel has been employed to derive a kernel function corresponding to an infinite-width neural network, providing valuable theoretical insights into neural network learning.

Domingo’s paper reveals a noteworthy connection between models learned through gradient descent and kernel-based techniques: during training, the training data is implicitly retained within the network weights. During inference, this retained training data collaborates with the nonlinear transformations of the neural network to compare new data against previously encountered examples, mirroring the functionality of kernel methods.

While the full implications of this relationship are still unclear, they may help explain why gradient descent-trained neural networks struggle with o.o.d. learning: if they depend heavily on memory, they might perform poorly in generalization unless taught to forget certain information (i.e., through regularization). This insight could inform strategies for enhancing model regularization for improved generalization.

Memory pertains to the storage and retrieval of information over time, making it a significant aspect of time series analysis. Recurrent Neural Networks (RNNs) and Long Short-Term Memory Networks (LSTMs) are two prevalent architectures for modeling time series data.

A traditional benchmark for memory in sequence models is the addition problem, where a model must sum two numbers presented at different time points and provide the correct result at a later time. This necessitates retaining information across extended periods, which becomes increasingly challenging as the time intervals between inputs grow. This challenge is linked to the vanishing and exploding gradient problem, which arises from the repetitive application of the same layer during backpropagation across sequence models. This often leads to models that are either costly to train or untrainable for certain tasks.

The difficulty of maintaining memory is associated with learning slow time scales. Research shows that addition problems can be effectively resolved by establishing subspaces of slow dynamics within an RNN, known as line attractors, allowing stable information retention without interference from the broader network dynamics.

LSTMs, renowned as the most cited neural network architecture of the 20th century, address the memory challenge by incorporating a cell state that can retain information over arbitrary durations, along with input, output, and forget gates that manage information flow. Consequently, LSTMs outperform traditional RNNs in retaining information across extensive time steps and excelling at tasks like the addition problem.

Nonetheless, as previously noted, memory can have drawbacks: it may facilitate overfitting by merely recalling information instead of achieving comprehension through compression.

The language of dynamical systems provides a physicist’s framework for discussing temporal phenomena. Descriptions of reality through differential equations are foundational to many physical theories, from Newton's laws to Schrödinger's equation.

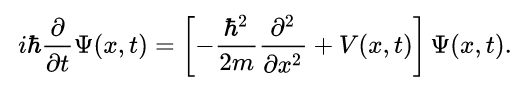
These descriptions are characterized by their memoryless nature. Given an initial state and a complete description of the system's time evolution operator (its Hamiltonian), the system’s evolution can be predicted indefinitely, even allowing for time reversal without loss of information. Thus, memory becomes unnecessary; if the description is comprehensive, it is optimally compressed in terms of Kolmogorov complexity.

In the field of dynamical systems reconstruction, which involves recovering a dynamical system from time series data, models with memory can hinder progress by failing to generalize to the true system dynamics, opting instead to overfit by memorizing spurious patterns in the training data. This presents a significant challenge for learning models of complex dynamical systems, such as the brain or climate, where accurately generalizing to a description that captures long-term behavior is vital for practical applications like predicting dynamics post-tipping points. Such understanding is crucial for forecasting extreme weather events or assessing the long-term impacts of climate change. However, the inherent noise and chaos of real-world systems complicate the task of distinguishing signal from noise.

In many practical scenarios, we lack a comprehensive understanding of the world around us. Utilizing memory, especially when a more compressed reality description is unavailable or impractical, remains essential for constructing intelligent systems and is a defining trait of human intelligence. Nonetheless, exploring the interplay between generalization and memory may yield insights for designing algorithms that achieve superior generalization.