Exploring Double Summation: A Math Challenge Unveiled
Written on
Chapter 1 Understanding Summation Techniques
Imagine you need to calculate the sum of all integers from 1 to 100. You could pair the numbers: 1 with 100, 2 with 99, and so on. This method leads to the formula of 101 multiplied by 50, which accounts for the total pairs.
What if we ventured into a more intricate expression like this? Here’s a suggestion: revisit the introduction for insights.
Take a moment to pause, grab your pen and paper, and challenge yourself with this problem. Once you're ready, continue reading for the solution!
Solution
We recognize that the total of the first 100 positive integers is given by a specific formula.

Next, we need to clarify the double summation expression.
We can begin by separating i and j and redistributing the double summation like this:
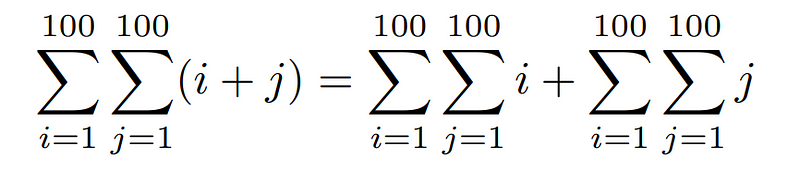
Now, let’s concentrate on the right side of the equation. We will first rearrange the two summations for i.
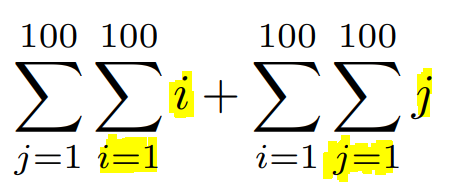
You might notice that in the first term’s j summation and the second term’s i summation, there are no corresponding variables present. By convention, we consider it as simply summing 1 for 100 instances, yielding 100.
Thus, our expression simplifies to:
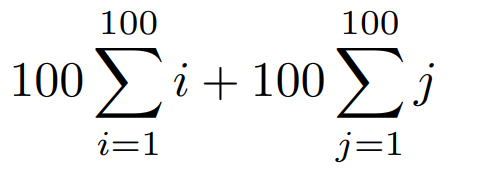
As noted earlier, the sum from 1 to 100 equals 5050, leading us to:

And there you have it! Isn’t that fascinating?
What thoughts crossed your mind during this exercise? Feel free to comment below; I’d love to hear your insights!
Math Puzzles
Explore a collection of engaging math puzzles available on Medium, covering topics like Algebra, Geometry, Calculus, and Number Theory. Share your favorites with friends!
The first video, How to Solve Double Summations (Steps), provides a detailed guide on tackling double summation problems, enhancing your problem-solving skills.
The second video, How to do double summation, offers a practical approach to understanding double summation techniques, making complex topics more accessible.
Thank you for taking the time to read this! If you found it helpful, don’t forget to applaud the article.

If you feel generous, consider buying me a coffee to support my writing journey. Your kindness means a lot!
Love, Bella 😊