Positive Rationals and Primes

The operations of addition (+) and multiplication (×) exhibit a delightful relationship, as noted by the distributive property: a × (b + c) = a × b + a × c. Both operations are associative, meaning that for addition, for instance, a + (b + c) = (a + b) + c, and they are commutative, as demonstrated by a + b = b + a.

This article will delve into a significant subset of the rationals, specifically the positive fractions, denoted as ??. It's crucial to note that ?? does not form a subfield of ? because, with respect to addition, ?? does not satisfy the criteria of an Abelian group. However, it does indeed represent a subgroup of the non-zero rationals under multiplication.

If you're unfamiliar with the concept of an Abelian group, you can think of it as a generalization of integers, wherein every integer n has an additive inverse -n that sums to yield the additive identity 0. Similarly, the set of positive fractions constitutes an Abelian group concerning multiplication, as each number r possesses a reciprocal 1/r, which, when multiplied together, results in the multiplicative identity 1.

> You don't need prior knowledge of group theory or ring theory to continue. Feel free to skip any sections that mention these concepts; you'll still be able to follow along without difficulty.

It is noteworthy that any well-defined operation on the group ?? naturally extends to the natural numbers, denoted by ?. We define natural numbers as the positive whole numbers, excluding 0. While the group ?? lacks a unique decomposition into primes like ?, both numerators and denominators do possess such decompositions. This fact stems from the Fundamental Theorem of Arithmetic, which asserts that any natural number n > 1 can be uniquely factored into prime numbers. For instance, 15/14 can be expressed as 3×5 / 2×7.

Prime numbers serve as an infinite basis for natural numbers, in the sense that every number can be represented as a product of primes, with at most one unique factorization for each number. This concept bears resemblance to a basis in a vector space, where a basis spans the space and remains linearly independent. Hence, we can draw parallels between products and primes in the realm of fractions and vectors in a vector space.

A Polynomial Bridge Between Worlds

Next, we will denote the ring of polynomials with integer coefficients as ?[x]. An example of such a polynomial is f(x) = -x³ + 3x² - 2. We will define a mapping Q between the two Abelian groups ?? and ?[x], where the latter is viewed as a group under polynomial addition and the former as a group under multiplication.

Let n > 1 be a natural number with the following prime factorization:

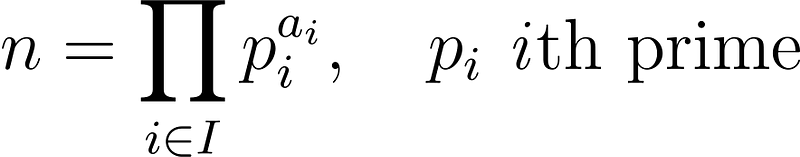
Here, I ? ? represents a finite subset of natural numbers. We can define a function P: ? ? ?[x] that maps the number n to the polynomial:

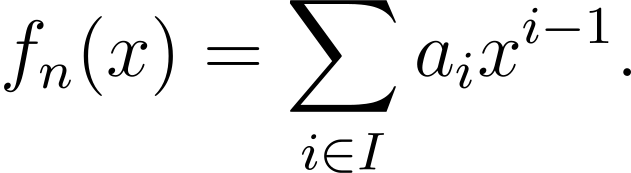
By convention, we will set f(1) = 0. For example, the number 18 can be factored as 2¹×3², where 2 is the first prime and 3 is the second prime, thus yielding:

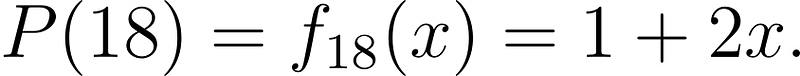
Similarly, P(10) results in 1 + x², as the constant term 1 corresponds to the prime 2, and x² corresponds to the prime 5. For P(9), we find 2x, since x corresponds to the prime 3, and the coefficient 2 indicates the exponent in 3² = 9.

Thus, we can assign a polynomial to each natural number, which is a significant finding. However, I promised to show you the mapping Q from ?? to ?[x]. We define Q as follows: Q(n/m) = P(n) - P(m).

For example, Q(14/3) yields P(14) - P(3) = 1 + x³ - x = 1 - x + x³. The remarkable aspect of this function is its property: Q(r × s) = Q(r) + Q(s) for any r, s ? ??. This characteristic defines a group homomorphism, establishing that Q functions as a homomorphism from the group of positive fractions to the group of polynomials with integer coefficients.

Since ? is defined as a set of equivalence classes of fractions with equal decimal values, the homomorphism Q is also bijective, meaning it acts as an isomorphism. Consequently, products of numbers within ?? correspond exactly to sums of polynomials in ?[x] in a one-to-one manner. Moreover, each polynomial with integer coefficients finds a corresponding counterpart in the realm of positive fractions, and vice versa.

This relationship is akin to a bridge connecting two realms, enabling us to translate knowledge from one into the other. For instance, let’s compute (3/2) × (4/5) within the polynomial framework:

Q((3/2) × (4/5)) = Q(3/2) + Q(4/5) = x - 1 + 2 - x² = 1 + x - x².

To interpret this outcome within the parallel universe of fractions, we must apply the inverse of Q to the result, denoting this inverse mapping as S. Thus, we find (3/2) × (4/5) = S(1 + x - x²) = 2 × 3 / 5 = 6/5.

A New Product

This isomorphism holds intrinsic interest, and I will certainly explore it further in subsequent writings. However, we must progress because, as promised, there is an operation to define. Currently, we have only utilized ?[x] as an Abelian group under addition, but it possesses additional structure as a ring. This means that it also has a well-defined product operation with specific rules and properties.

Our isomorphism Q allows us to interpret products of fractions as sums of polynomials and vice versa. But how do we interpret the product of polynomials in the context of fractions? We will establish a binary operation ? on the positive fractions. This notation is utilized in other mathematical contexts, such as tensor products, but should not be confused with those.

We define this operation as follows:

r ? s = S(Q(r) × Q(s)), where S is the inverse of Q.

For example, consider 6 ? 15 = S((1 + x) × (x + x²)) = S(x + 2x² + x³) = 3 × 5² × 7 = 525. The unique aspect of this operation is its distributive nature over multiplication: a ? (b × c) = (a ? b) × (a ? c).

Let’s revisit our earlier example. Recognizing that 15 = 3 × 5, we can calculate 6 ? 15 as follows: 6 ? (3 × 5) = (6 ? 3) × (6 ? 5) = S(x + x²) × S(x² + x³) = 15 × 35 = 525. While this may seem redundant, revisiting examples aids in comprehension.

Polynomial Primes

In the realm of natural numbers, we are fortunate to have prime numbers acting as multiplicative atoms. But does this concept extend to our newly defined operation in the positive fractions? The answer is a resounding yes. In fact, this characteristic is inherited from the unique factorization theorem in the ring ?[x].

For instance, the fraction 2/5 can be expressed uniquely in terms of the product as follows:

2/5 = 2/3 ? 6, and this is the sole way to factor it. This mirrors the expression (1 - x²) = (1 - x)(1 + x).

Thus, we have a fundamental theorem of arithmetic pertaining to this operation, indicating the existence of fractional primes under this operation. Though this discussion could continue indefinitely, I encourage you to explore this topic further on your own.

If you discover anything intriguing, please share your findings. To access an endless array of stories like this, click here and join our community.